Rabu, 25 Januari 2017
Jumat, 13 Januari 2017
latihan un 1
- 17 - ( 3 x (-8) adalah ....
A.49
B.41
C.-7
D.-41
- Hasil dari : (-20) + 8 x 5 - 18 : (-3) = ...
A.-26
B.-14
C.14
D.26
- Hasil dari : -24 + 72 : (-12) - 2 x (-3) = ....
A.-24
B.-18
C.18
D.24 - Hasil dari : -6 + (6 : 2) - [(-3) x 3 ] adalah. . .
A.0
B.3
C.6
D.9 - Hasil dari : 25 - ( 8 : 4) + (-2 x 5) adalah ...
A.-33
B.-13
C.13
D.33
- Pada lomba Matematika ditentukan untuk jawaban yang benar mendapat skor 2, jawaban salah mendapat skor -1, sedangkan bila tidak menjawab mendapat skor 0. Dari 75 soal yang diberikan, Yuli menjawab 50 soal dengan benar dan 10 soal tidak dijawab. Skor yang diperoleh Hammam adalah....
A.120
B.100
C.90
D.85 - Suhu di Jakarta 29C. Pada saat yang sama suhu di kutub utara -15C. Perbedaan suhu di kedua tempat tersebut adalah .... C.
A.44
B.14
C.-14
D.-44 - Jumlah tiga bilangan genap berurutan adalah 162. Jumlah bilangan terbesar dan terkecil adalah ....
A.108
B.106
C.104
D.102 - Jumlah tiga bilangan genap berurutan adalah 96. Jumlah bilangan terbesar dan terkecil adalah ....
A.56
B.62
C.64
D.68 - Jumlah tiga bilangan ganjil berurutan adalah 39. Jumlah bilangan terbesar dan terkecil dari bilangan tersebut adalah ....
A.22
B.24
C. 26
D.28 - bu Sumi membeli 40 kg beras. Jika rata-rata pemakaian beras setiap hari kg, maka beras tersebut akan digunakan dalam waktu ...
A.30 hari
B.32 hari
C. 40 hari
D.50 hari - Kebun dengan luas 800 m2 . Akan ditanami jagung 1/4 bagian dan ditanami pepaya 3/5 bagian. Jika sisanya akan ditanami singkong, maka luas kebun yang ditanami singkong adalah .... m2
A.120
B.180
C.200
D.480 - Tali yang panjangnya 12 meter akan dipotong menjadi beberapa bagian yang sama panjang. Jika tiap bagian panjangnya seperempat meter, maka banyak potongan tali yang terjadi adalah....
A.48
B.36
C.4
D.3 - Sebuah dadu dilambungkan satu kali. Peluang munculnya mata dadu lebih dari 4 adalah ....
A.1/6
B.1/4
C.1/3
D.2/3 - Dalam kotak terdapat 4 bola kuning, 14 bola warna merah, dan 6 bola warna hijau. Sebuah bola diambil secara acak, maka peluang terambil bola warna kuning adalah .....
A.1/14
B.1/6
C.1/5
D.1/4 - Bila peluang hari ini turun hujan 0,26, maka besar peluang hari ini tidak turun hujan yaitu sebesar ....
A.- 0,74
B.- 0,26
C.0,74
D.1,26 - Seperangkat kartu bridge sebanyak 52 kartu dikocok kemudian diambil 1 secara acak, maka peluang terambil kartu AS daun merah sebesar .....
A.1/13
B.1/14
C.1/16
D.1/26 - Empat keping uang logam dilempar sekali secara bersama-sama, maka peluang munculnya 3 gambar dan 1 angka adalah ....
A.1/2
B.1/4
C.1/8
D.1/32 - Suatu barisan aritmatika diketahui suku ke–4 adalah 14 dan suku ke–10 adalah 38, maka suku ke–20 adalah ....
A.70
B.74
C.78
D.82
- Suatu pekerjaan dapat diselesaikan oleh 15 orang pekerja dalam waktu 12 minggu. Jika pekerjaan itu harus selesai dalam waktu 9 minggu, maka banyak pekerja yang harus ditambah adalah ….
A.3 orang
B.4 orang
C.5 orang
D.20 orang
- Bejo meminjam uang untuk modal di sebuah bank sebesar Rp1.800.000,00. Jika bank itu menetapkan suku bunga pinjaman sebesar 9% per tahun dan Bayu membayar pinjaman itu dengan mengangsur sebesar Rp193.500,00, maka lama pinjaman Bayu di bank itu adalah ...
A.10 bulan
B.9 bulan
C.8 bulan
D.6 bulan - Pada barisan aritmetika, diketahui U5 = 16 dan U11 = 34. Jumlah 40 suku pertama barisan bilangan tersebut adalah ....
A.2.500
B.2.420
C.2.000
D.1.360 - Dalam sebuah aula terdapat 10 kursi pada baris pertama dan setiap baris berikutnya bertambah 4 kursi dari baris di depannya. Jika aula tersebut memuat 16 baris kursi, maka banyaknya kursi di aula tersebut adalah ....
A.615 kursi
B.640 kursi
C.720 kursi
D.870 kursi - Perhatikan pernyataan di bawah ini!
(i) x2 – 4 = (x + 2)(x – 2)
(ii) 3x2 + 6x = 3x (2x + 3)
(iii) 2x2 + 3x – 2 = (2x + 1)(x – 2)
(iv) x2 + 2x – 15 = (x + 5)(x – 3)
Pernyataan yang benar adalah ….
A.(i) dan (ii)
B.(ii) dan (iii)
C.(iii) dan (iv)
D.(i) dan (iv)
- Jika 3x + 3 = –2x + 18, maka nilai x + 1 adalah ....
A.3
B.4
C.5
D.6 - Sebuah persegipanjang berukuran panjang (2x + 1) cm dan lebar (x – 2) cm. Jika kelilingnya 40 cm, maka luasnya adalah ....
A.64 cm2
B.75 cm2
C.91 cm2
D.96 cm2 - Dari 30 warga ditanya mengenai minuman kegemarannya. 25 orang gemar minum teh dan 12 orang gemar minum teh dan kopi. Banyaknya warga yang gemar minum kopi adalah ....
A.17 orang
B.13 orang
C.7 orang
D.5 orang - Jika f(x) = 4x – 3 dan f(d) = 17, maka nilai d adalah ....
A.5
B.6
C.8
D.9 - Persamaan garis yang melalui titik T(–3, –4) dan tegak lurus dengan garis yang melalui titik (2, –2) dan (–2, –8) adalah ..
A.3y + 2x = –6
B.2y + 3x = 6
C.3y + 2x = –18
D.2y + 3x = 18 - Diketahui titik K(3, 1), L(–1, –2), dan M(–4, r). Jika garis yang melalui titik KL tegak lurus dengan garis yang melalui titik LM, maka nilai r adalah ….
A.-4
B.-2
C.2
D.4 - Pada sebuah tempat parkir terdapat 84 kendaraan yang terdiri atas sepeda motor dan mobil. Setelah dihitung, jumlah roda seluruhnya ada 220. Jika tarif parkir parkir untuk sepeda motor Rp1.000,00 dan untuk mobil Rp2.000,00, besar uang parkir yang diterima tukang parkir tersebut adalah ….
A.Rp 220.000,00
B.Rp 168.000,00
C.Rp 110.000,00
D.Rp 84.000,00 - Sudut A dan sudut B adalah dua sudut yang saling berpelurus. Jika besar ÐA = (3x + 5)o dan besar ÐB = (3x + 7)o, maka besar ÐB adalah ....
A.28 derajat
B.89 derajat
C.91 derajat
D.119 derajat - Sebuah lingkaran berpusat di titik O dengan panjang jari-jari 14 cm. Jika besar ÐCOD = 90o, maka panjang busur CD adalah ....
A. 20 cm
B.22 cm
C.24 cm
D. cm - Diketahui dua lingkaran masing-masing berjari-jari 11 cm dan 4 cm. Jika panjang garis singgung persekutuan luar lingkaran 24 cm, maka jarak titik pusat kedua lingkaran tersebut adalah ....
A.23 cm
B.24 cm
C.25 cm
D.26 cm - Sebuah limas mempunyai alas berbentuk segi-6. Banyaknya rusuk dan sisi limas berturut-turut adalah ....
A.12 dan 7
B.12 dan 8
C.18 dan 7
D.18 dan 8 - Volume prisma yang alasnya berbentuk layang-layang dengan panjang diagonal 10 cm dan 14 cm serta tinggi prisma 15 cm adalah ....
A.140 cm3
B.700 cm3
C.1.050 cm3
D.2.100 cm3 -
Peluang munculnya mata dadu berjumlah 7 pada percobaan melempar undi dua dadu bersama-sama sebanyak satu kali adalah ...
A.7/36
B.6/36
C. 5/36
D.4/36 - Perhatikan gambar di bawah !
Bangun KLMN adalah persegi panjang dan RSTU adalah persegi ,diketahui luas daerah diarsir 256 cm2,luas daerah yang tidak di arsir adalah . . . . .
A.1.760 cm2
B.1.504 cm2
C.880 cm2
D.504 cm2 - Sebuah kebun berukuran panjang 64 m dan lebar 48 m,disekeliling kebun dipasangi pagar bambu dengan jarak antar ruas bambu 25 cm, jumlah ruas bambu yang diperlukan adalah . . . .
A.112
B.224
C.448
D.896 - Perbandingan panjang dan lebar persegi panjang adalah 5 : 3 ,jika keliling persegi panjang tersebut 128 cm, maka selisih panjang dan lebarnya adalah . . . .
A.8 cm
B.16 cm
C.24
D.40 cm
Rabu, 11 Januari 2017
soal barisan dan deret
- Pola bilangan 2,6,m,20,30,42, . . . akan terbentuk jika m = . . . . .
a.10
b.12
c.14
d.16 - Diketahui bilangan 5,8,13,20, . . . . . tiga suku berikutnya adalah . . . .
a.28,40,50
b.28,40,53
c.29,40,53,
d.29,42,54 - Jumlah bilangan ganjil dari 7 sampai dengan 23 adalah . . . .
a.123
b.135
c.149
d.152 - bilangan yang belum diketahui dari barisan bilangan 3,6,11,20,37,. . .,135 adalah . . . .
a.51
b.53
c.70
d.86 - Pada susunan bilangan segitiga pascal jumlah bilangan yang terdapat pada baris ke 10 adalah . . . .
a.128
b.256
c.512
d.1024 - Jika (a + b)5= a5+pa4b+qa3b2+ra2b3+sab4+b5 maka nilai dari 5p - 2q + 3r adalah . . . .
a.35
b.37
c.42
d.48 - Perhatikan pola bilangan berikut !
Zaenal menyusun kelereng seperti gambar diatas banyaknya pola ke 7 adalah . . . .
a.27
b.28
c.29
d.31
- Perhatikan gambar di atas ! tersusun atas batang batang lidi,banyaknya segitiga kecil pada pola ke 7 adalah . . . .
a.45
b.49
c.54
d.59
- Perhatikan pola berikut !
Pola bilangan yang menyatakan banyak titik pada pola diatas adalah . . . .
a.1,5,9,13,16, . . .
b.1,5,9,13,17, . . .
c.1,5,9,14,18,. . .
d.1,5,9,14,19, . . .
- Dari susunan bilangan berikut susunan bilangan yang bukan tergolong barisan bilangan adalah . . . .
a.1,5,9,13,. . .
b.5,12,20,29,. . . .
c.6,8,13,16,. . . .
d.10,21,33,46, . . .
- Perhatikan pola bilangan berilkut 12,9,5,m,-6,n,. . . .
nilai 2m + n = . . . .
a.-5
b.-6
c.-7
d.-13 - Dua suku berikutnya dari barisan bilangan 2,5,10,17,. . . adalah. . .
a.11 dan 13
b.25 dan 36
c.26 dan 37
d.37 dan 49 - Suku ke 16 dari barisan 3,-3,-9,-15, . . . adalah. . .
a.-81
b.-87
c.-93
d.-99 - Rumus suku ke n dari barisan 1,5,9,13,. . . .adalah . . . .
a.n(2n-1)
b.2n2-2
c.n(n+2)
d.4n-3 - Diketahui barisan bilangan 1,1,1,2,2,3,3,4,5,5,8,6,13,7,21,. . . .dua suku berikutnya dari barisan bilangan tersebut adalah . . . .
a.35 dan 9
b.34 dan 8
c.24 dan 9
d.24 dan 8 - Rumus suku ke n dari barisan bilangan 3,4,7,12,. . . .adalah . . . .
a.Un=n2+2n-4
b.Un=n2-2n+4
c.Un=2n+1
d.Un=2n2+n - Suku ke n dari barisan 1,3,6,10,15,21 adalah . . . .
a.1/4 n2
b.3n2
c.1/2 n(n-2)
d.1/2 n(n-3) - Diberikan barisan bilangan 3,5,9,15,23,. . . .,berapakah suku ke 16 ?
a.212
b.243
c.214
d.178
- Rumus suku ke n suatu barisan adalah Un=n2-2n jumlah suku ke 10 dan ke 11 barisan itu adalah . . . .
a.179
b.189
c.191
d.196 - Pernyataan berikut yang benar adalah . . . . a.3,7,11,15 adalah barisan bilangan yang terdiri atas 4 suku dan rumus suku ke n =4n + 1
- Perhatikan 3 barisan yang terdiri atas 6 bilangan berikut
1)8,16,32,64,128dan 256
2)7,11,16,22,29,dan37
3)2,9,2,16,2 dan 25
manakah dari 3 barisan tersebut yang menjadi 6 suku berikutnya dari suatu barisan bilangan yang tiga suku pertamanya 1,2 dan 4
a.1
b.2
c.3
d.semuanya - Sebuah tangga mempunyai anak tangga dengan ketinggian dari lantai 25 cm,45 cm, 65 cm, . . . . jika tangga tersebut mempunyai 15 anak tangga ketinggian anak tangga terakhir dari lantai adalah . . . .
a.3,35 cm
b.3,20 cm
c.3,15 cm
d.3,05 cm - Dari barisan barisan di bawah ini ,barisan aritmatika di tunjukkan oleh . . . .
a.-2,-6,-18,-54,. . . .
b.-2,0,2,4,6, . . . .
c.16,8,4,2,1,. . . .
d.1,3,9,27, . . . - Jika m dan n anggota dari barisan aritmatika 16,19,m,25,28,n,34,. . . .
maka 2m + n = . . .
a.22
b.42
c.53
d.75 - Suku ke 12 dari barisan aritmatika dengan rumus suku ke n, Un=18 +3n adalah . . . .
a.36
b.45
c.54
d.72 - Rumus suku ke n dari barisan 1,-4,-9,-14 ,. . . . adalah . . . . .
a.1 - 4n
b.5n - 4
c.4n - 5
d.6 - 5n - Terdapat barisan m + 20, (2(m - 5)+1, agar barisan tersebut membentuk barisan aritmatika maka nilai m adalah . . . .br/>a.31
b.20
c.11
d.10 - Jika di ketahui barisan aritmatika -18,-22,-26,-30, . . . maka U20 + U22 =. . . .
a.8
b.-94
c.-102
d.-196 - Diketahui brisan bilangan 2,5,8,11,14,. . . .suku ke 50 dari barisan tersebut adalah . . .
a.146
b.147
c.149
d.151 - Diketahui barisan aritmatika dengan suku ke 10 =8 dan beda 1/8 suku kedua dari barisan tersebut adalah . . .
a.7
b. 6 7/8
c.6 1/6
d. 1/8 - Diketahui suku ke 18 dan ke 30 dari suatu barisan aritmatika berturut turut 182 dan 314, beda barisan tersebut adalah . . .
a.12
b.11
c.-11
d.-12 - Dalam gedung pertunjukkan disusun kursi dengan baris pertama terdiri atas 12 buah,baris ke dua berisi 14 buah,baris ke tiga berisi 16 buah dan seterusnya bertambah 2, banyak kursi pada baris ke 20 adalah . . . .
a.28 buah
b.50 buah
c.58 buah
d.60 buah - Jumlah 20 suku pertama dari deret 6 + (-2) + (-10) + (-18) + . . . adalah . . .
a.1.400
b.140
c.-140
d.-1.400 - Suku pertama suatu deret aritmatika adalah -3 jika beda deret tersebut 4, jumlah 15 suku pertama deret tersebut adalah . . . .
a.750
b.500
c.375
d.75 - Diketahui deret 18 + 11 + 4 + (-3) + . . . . jumlah 15 suku pertama dari deret tersebut adalah . . . .
a.-458
b.-465
c.-472
d.-479 - Jumlah bilangan bulat antara 4 dan 99 yang habis dibagi 5 adalah . . . .
a.950
b.945
c.900
d.850 - Dalam suatu deret aritmatika suku ke 1 adalah 8 dan suku ke 4 adalah 23 jumlah 19 suku pertama dari deret tersebut adalah . . . .
a.995
b.997
c.1.005
d.1.007 - Ali menabung di koperasi sekolah pada bulan januari ia menabung Rp 7.500,--bulan pebruari Rp 10.000,--,bulanmaret Rp 12.500,--dan seterusnya jumlah tabungan Ali sampai akhir bulan desember adalah . . . .
a.Rp 250.000
b.Rp 255.000
c.Rp 260.000
d.Rp 275.000 - Diketahui sebuah deret aritmatika dengan jumlah n suku pertama dirumuskan Sn = 4n2 + n maka beda (b) deret itu adalah . . . .
a.Un= 8n - 1
b.Un= 8b + 2
c.Un=4n + 1
d.Un=4n + 3 - Jika jumlah n suku pertama deret aritmatika ditentukan oleh Sn = n2 + n maka beda (b) deret tersebut adalah . . . .
a.8
b.4
c.3
d.2 -
Diketahui deret : 3 + 5 + 7 + 9 + ....jumlah 5 suku yang pertama adalah....
a.24
b,25
c.35
d.40
e.48
- Diketahui barisan aritmatika suku ke-4 = 17 dan suku ke-9 = 39. Suku ke-41 adalah....
a.165
b.169
c.185
d.189
e.209 - iketahui barisan aritmatika 27,24, 21, ....
Jumlah 20 suku pertama adalah....
a.-60
b.-30
c.540
d.840
e.1.100 - 27, 64, 18, 48, 12, 36, .....dua suku berikut adalah . . .
a.8, 27
b.8, 25
c.6, 27
d.6, 25
- Suatu jenis bakteri, setiap detik akan membelah diri menjadi dua. Jika pada saat permulaan ada 5 bakteri, waktu yang diperlukan bakteri supaya menjadi 320 adalah .....
a.5 detik
b.6 detik
c.7 detik
d.16 detik - Sebuah bola jatuh dari ketinggian 10 m dan memantul kembali dengan ketinggian ¾ kali tinggi sebelumnya, begitu seterusnya hingga bola berhenti.Jumlah seluruh lintasan bola adalah .....
a.65 m
b.70 m
c.75 m
d.77 m - Suku ke-5 sebuah deret aritmatika adalah 11 dan jumlah nilai suku ke-8 dengan suku ke-12 sama dengan 52. Jumlah 8 suku pertama deret tersebut ialah …..
a. 68
b. 72
c. 76
d. 80
- Seorang petani memetik buah coklat setiap hari dan mencatatnya, ternyata banyak buah coklat yang dipetik pada hari ke-n memenuhi Un = 30 + 10n.Banyaknya buah coklat yang dipetik selama 20 hari pertama adalah....a. 1.900 buahb. 2.300 buahc. 2.700 buahd. 2.760 buahd. 2.840 buah
- Seorang pemilik kebun memetik jeruknya setiap hari, dan mencatat banyaknya jeruk yang dipetik. Ternyata banyaknya jeruk yang dipetik pada hari ke-n memenuhi rumus Un = 50 + 25n. Jumlah jeruk yang yang telah dipetik selama 10 hari yang pertama adalah....a. 2.000 buahb. 1.950 buahc. 1.900 buahd. 1.875 buahe. 1.825 buah
- Diketahui barisan aritmatika U5 = 5 dan U10 = 15. Suku ke-20 barisan tersebut adalah....a. 320b. 141c. 35d. -35e. -41
- Dari suatu barisan aritmatika diketahui U10 = 41 dan U5 = 21. U20 barisan tersebut adalah....A. 69B. 73C. 77D. 81E. 83
- Dari suatu barisan aritmatika diketahui suku keempat adalah 7 dan jumlah suku keenam dan ke delapan adalah 23. besar suku keduapuluh adalah....a. 21b. 30c. 31d. 41e. 60
- Diketahui barisan aritmatika suku kelima 21 dan suku kesepuluh 41, suku kelimapuluh barisan aritmatika tersebut adalah....a. 197b. 198c. 199d. 200e. 201
- Suku kesepuluh dan ketiga suatu barisan aritmatika berturut-turut adalah 2 dan 23. Suku keenam barisan tersebut adalah....a. 11b. 14c. 23d. 44e. 129
- Barisan aritmatika suku ketiga = 16 dan suku keenam = -7, maka suku kedelapan = ....a. 1b. 10c. 22d. 64e. 92
- Jumlah semua bilangan genap antara 10 dan 100 yang habis dibagi 3 adalah....a. 810b. 864c. 1.665d. 2.420e. 2.530
- Jika suku pertama suatu barisan geometri = 16 dan suku ketiga = 36, maka besar suku kelima adalah....a. -81b. -52c. -46d. 46e. 81
- Seorang karyawan perusahaan diberi upah pada bulan pertama sebesar Rp 600.000,00. Karena rajin, jujur dan terampil maka pada setiap bulan berikutnya upahnya ditambah Rp 10.000,00. Upah karyawan tersebut pada bulan ke-12 adalah....a. Rp. 610.000,00b. Rp. 612.000,00c. Rp. 710.000,00d. Rp. 720.000,00e. Rp. 7.860.000,00
- Pada tahun pertama seorang karyawan mendapat gaji pokok Rp 300.000,00 sebulan. Jika setiap tahun gaji pokoknya dinaikkan sebesar Rp 25.000,00 maka jumlah gaji pokok tersebut selama 10 tahun pertama adalah....a. Rp. 37.125.000,00b. Rp. 38.700.000,00c. Rp. 39.000.000,00d. Rp. 41.125.000,00e. Rp. 49.500.000,00
- Diketahui barisan geometri dengan suku pertama = 4 dan suku kelima = 324, maka jumlah delapan suku pertama deret yang bersesuaian adalah....a. 6.560b. 6.562c. 13.120d. 13.122e. 13.124
- Adi memiliki kelinci yang setiap 3 bulannya bertambah menjadi 3 kali lipat. Jika banyak kelinci pada akhir bulan Maret 2003 diperkirakan mencapai 216 ekor, maka kelinci Adi pada akhir bulan juni 2002 adalah....a. 8 ekorb. 27 ekorc. 72 ekord. 200 ekore. 210 ekor
- Suatu deret aritmatika memiliki beda 2 dan jumlah 20 suku pertamanya 240. Jumlah tujuh suku pertamanya adalah …
- Jika suatu barisan geometri y + 1, 2y – 2, 7y – 1, ….. mempunyai rasio positif, maka suku ke-4 barisan tersebut adalah …..
- Dalam suatu deret aritmatika, jika U₃ + U₇ = 56 dan U₆ + U₁₀ = 86, maka suku ke-2 adalah …..
a. 8
b. 10
c. 12
d. 13
e. 15
- Diketahui suku ketiga dan suku kelima dari deret aritmatika berturut-turut adalah 18 dan 24. Jumlah tujuh suku pertamanya adalah …..
a. 117
b. 120
c. 137
d. 147
e. 160 - Agar deret geometri tak hingga dengan suku pertama a mempunyai jumlah 2, maka a memenuhi …..
a. -2 < a < 2
b. -4 < a < 0
c. 0 < a < 2
d. 0 < a < 4
e. -4 < a < 4 - Suku tengah suatu deret aritmatika adalah 23. Jika suku terakhirnya 43 dan suku ketiganya 13, maka banyaknya suku pada deret tersebut adalah …..
a. 5
b. 7
c. 9
d. 11
e. 13 - Suku ke-2 dari suatu deret aritmatika adalah 5. Jika jumlah dari suku ke-4 dan suku ke-6 dari deret terrsebut adalah 28, maka suku ke-9 adalah …..
a. 19
b. 21
c. 26
d. 28
e. 29 - Suku ke-5 dari barisan geometri adalah 243, hasil bagi suku ke-9 dengan ke-6 adalah 27. Suku ke-2 adalah …..
a. 3
b. 5
c. 7
d. 9
e. 11
b.3,5,7,9 adalah barisan dengan suku pertamanya 3 dan rumus suku ke n = 2n + 1
c.1,7,17,31 adalah barisan dengan suku ke limanya 49 dan rumus suku ke n = 2n2 + 1
d.3,8,11,15 adalah barisan yang terdiri dari 4 suku dan rumus suku ke n =(n + 1)2 - 1
a.-5
b. -6
c.-7
d.-8
e.-9
Jumat, 06 Januari 2017
BARISAN DAN DERET GEOMETRI
BARISAN GEOMETRI
Barisan geometri merupakan barisan yang suku-sukunya diperoleh dengan mengalikan satu bilangan tetap ke suku sebelumnya. Bilangan tetap itu sering disebut sebagai pembanding atau rasio yang dilambangkan dengan r.
Barisan U1 , U2 , U3 , U4 , ….. , Un disebut sebagai barisan geometri jika memenuhiRasio
Contoh barisan geometri :
7, 21, 63, 189, ....
3, 6, 12 , 24, 48 ,. . . .
Rumus Suku ke-n
Jika suku pertama ( U1 ) dari suatu barisan geometri disimbolkan dengan a , maka rumus suku ke-n barisan geometri dapat ditentukan sebagai berikut:
Dari pernyataan diatas, dapat ditarik kesimpulan bahwa rumus suku ke-n dari suatu barisan geometri adalah
Dimana r adalah rasio atau pembanding yang dapat dicari dengan cara berikut:

Contoh Soal :
DERET GEOMETRI
Jumlah dari n suku pertama suatu barisan geometri disebut sebagai deret geometri. Jika suku ke-n dari barisan geometri dirumuskan: an = a1rn – 1, maka deret geometri dapat dituliskan sebagai,
Jika kita mengalikan deret tersebut dengan –r kemudian menjumlahkannya dengan deret aslinya, kita mendapatkan
Sehingga kita memperoleh Sn – rSn = a1 – a1rn. Dengan menyelesaikan persamaan tersebut untuk Sn, kita mendapatkan
Rumus suku ke n

Contoh Soal:
1. Dari deret 32 + 16 + 8 + .... didapat a = 32 dan r = 1/2, sehingga
2. Dari deret 2 + 22 + 23 + ….. + 2n = 510 didapat a = 2 dan r = 2, sehingga
Soal No. 3
Diberikan sebuah deret geometri sebagai berikut.
3 + 6 + 12 + ....
Tentukan suku ke-5 dari deret tersebut!
Pembahasan
Rumus suku ke-n deret geometri
Un = arn −1
dimana
a = suku pertama
r = rasio
Dari soal
a = 3
r = 6/3 = 2
sehingga
Un = arn−1
U5 = 3 (2)5 −1 = 3 (2)4 = 3(16) = 48
Soal No. 4
Diketahui suku pertama suatu deret geometri adalah 4 dengan suku ke-5 adalah 324. Tentukan rasio dari deret tersebut!
Pembahasan
Data dari soal di atas
U5 = 324
a = 4
Dari Un = arn −1

Dengan demikian rasionya adalah 3 atau − 3
Soal No. 5
Deret geometri 12 + 6 + 3 + ....
Tentukan U3 + U5
Pembahasan
U3 = 3
a = 12
r = 6/12 = 1/2
Un = arn −1
U5 = 12(1/2)5 −1 = 12(1/2)4 = 12(1/16) = 12/16 = 3/4
Sehingga
U3 + U5 = 3 + 3/4 = 3 3/4
Soal No. 6
Diberikan sebuah deret geometri sebagai berikut.
3 + 6 + 12 + ....
Tentukan jumlah 7 suku pertama dari deret tersebut!
Pembahasan
Data:
a = 3
r = 6/3 = 2
S7 =....
Rumus mencari jumlah n suku pertama deret geometri untuk rasio lebih besar dari satu r > 1
Sehingga:


Soal No. 7
Diberikan sebuah deret geometri sebagai berikut.
24 + 12 + 6 +...
Tentukan jumlah 7 suku pertama dari deret tersebut!
Pembahasan
Data:
a = 24
r = 12/24 = 1/2
S7 =....
Rumus mencari jumlah n suku pertama deret geometri untuk rasio lebih kecil dari satu r < 1
Sehingga:


soal no 8

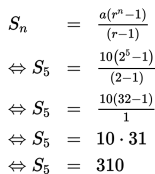

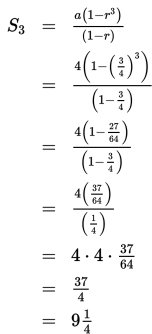
Barisan ini adalah barisan geometri turun dengan a = 3 dan r =34

Jadi, panjang lintasan yang terbentuk sampai bola menyentuh lantai untuk yang ke 3 kalinya adalah 14, 5 meter.
Latihan
Barisan geometri merupakan barisan yang suku-sukunya diperoleh dengan mengalikan satu bilangan tetap ke suku sebelumnya. Bilangan tetap itu sering disebut sebagai pembanding atau rasio yang dilambangkan dengan r.
Barisan U1 , U2 , U3 , U4 , ….. , Un disebut sebagai barisan geometri jika memenuhiRasio
Contoh barisan geometri :
7, 21, 63, 189, ....
3, 6, 12 , 24, 48 ,. . . .
Rumus Suku ke-n
Jika suku pertama ( U1 ) dari suatu barisan geometri disimbolkan dengan a , maka rumus suku ke-n barisan geometri dapat ditentukan sebagai berikut:
Dari pernyataan diatas, dapat ditarik kesimpulan bahwa rumus suku ke-n dari suatu barisan geometri adalah
Dimana r adalah rasio atau pembanding yang dapat dicari dengan cara berikut:
Contoh Soal :
- Tentukan suku ke tujuh dari barisan geometri 3, 6, 12, .....!
- Tentukan Rumus Suku ke-n dari barisan 48 , 24 , 12 , ……!
- Dari barisan geometri diketahui bahwa U3 = 4 dan U9 = 256, maka tentukan U12!
- Tiga buah bilangan membentuk barisan geometri. Jumlah ketiga bilangan tersebut sama dengan 35, sedangkan hasil kali ketiga bilangan itu sama dengan 1.000. Maka tentukan barisan geometri tersebut!
- Dari Barisan 3, 6, 12, ... didapat a = 3 dan r = 6/3 = 2 sehingga,
Un = a.rn-1
U7 = 3.2
U7 = 3.26
U7 = 3.64
U7 = 192
- Dari barisan 48, 24, 12, .... didapat a = 48 dan r = 24/48 = 1/2 sehingga,
- Pertama, kita jabarkan terlebih dahulu U3 dan U9 kemudian kita cari nilai rasionya
U3 = 4 → a.r2 = 4
U9 = 256 → a.r8 = 256 - jawaban soal no 4
Un = a.rn-1
Un = 48.(1/2)n-1
Un = 48.(1/2)n-1
Un = 48.(2-1)1-n
Un = 3.16.(2)1-n
U7 = 3.24(2)1-n
U7 = 3.25-n
Kemudian substitusikan untuk mencari U1 atau a!
→ a.r2 = 4
→ a.22 = 4
→ a = 1
Next, cari nilai U12 dengan menggunakan rumus umum barisan geometri!
U12 = a.rn-1
U12 = 1.211
U12 = 1.2048
U12 = 2048
DERET GEOMETRI
Jumlah dari n suku pertama suatu barisan geometri disebut sebagai deret geometri. Jika suku ke-n dari barisan geometri dirumuskan: an = a1rn – 1, maka deret geometri dapat dituliskan sebagai,
Jika kita mengalikan deret tersebut dengan –r kemudian menjumlahkannya dengan deret aslinya, kita mendapatkan
Sehingga kita memperoleh Sn – rSn = a1 – a1rn. Dengan menyelesaikan persamaan tersebut untuk Sn, kita mendapatkan
Rumus suku ke n

Contoh Soal:
- Tentukan jumlah 10 suku pertama dari deret 32 + 16 + 8 + ….!
- Tentukan nilai n yang memenuhi2 + 22 + 23 + ….. + 2n = 510!
1. Dari deret 32 + 16 + 8 + .... didapat a = 32 dan r = 1/2, sehingga
2. Dari deret 2 + 22 + 23 + ….. + 2n = 510 didapat a = 2 dan r = 2, sehingga
Soal No. 3
Diberikan sebuah deret geometri sebagai berikut.
3 + 6 + 12 + ....
Tentukan suku ke-5 dari deret tersebut!
Pembahasan
Rumus suku ke-n deret geometri
Un = arn −1
a = suku pertama
r = rasio
Dari soal
a = 3
r = 6/3 = 2
sehingga
Un = arn−1
U5 = 3 (2)5 −1 = 3 (2)4 = 3(16) = 48
Soal No. 4
Diketahui suku pertama suatu deret geometri adalah 4 dengan suku ke-5 adalah 324. Tentukan rasio dari deret tersebut!
Pembahasan
Data dari soal di atas
U5 = 324
a = 4
Dari Un = arn −1

Dengan demikian rasionya adalah 3 atau − 3
Soal No. 5
Deret geometri 12 + 6 + 3 + ....
Tentukan U3 + U5
Pembahasan
U3 = 3
a = 12
r = 6/12 = 1/2
Un = arn −1
U5 = 12(1/2)5 −1 = 12(1/2)4 = 12(1/16) = 12/16 = 3/4
Sehingga
U3 + U5 = 3 + 3/4 = 3 3/4
Soal No. 6
Diberikan sebuah deret geometri sebagai berikut.
3 + 6 + 12 + ....
Tentukan jumlah 7 suku pertama dari deret tersebut!
Pembahasan
Data:
a = 3
r = 6/3 = 2
S7 =....
Rumus mencari jumlah n suku pertama deret geometri untuk rasio lebih besar dari satu r > 1
Sehingga:


Soal No. 7
Diberikan sebuah deret geometri sebagai berikut.
24 + 12 + 6 +...
Tentukan jumlah 7 suku pertama dari deret tersebut!
Pembahasan
Data:
a = 24
r = 12/24 = 1/2
S7 =....
Rumus mencari jumlah n suku pertama deret geometri untuk rasio lebih kecil dari satu r < 1
Sehingga:


soal no 8
Seutas tali dibagi menjadi 5 bagian yang panjangnya membentuk barisan geometri.
Jika tali yang paling pendek adalah 10 cm dan tali yang paling panjang adalah 160 cm, tentukan panjang tali semula.
Jika tali yang paling pendek adalah 10 cm dan tali yang paling panjang adalah 160 cm, tentukan panjang tali semula.
Penyelesaian:
Diketahui potongan-potongan tali membentuk barisan geometri, dengan:
panjang tali terpendek = U1 = a = 10
panjang tali terpanjang = U5 = ar4 = 160
banyak bagian tali = n = 5
panjang tali terpendek = U1 = a = 10
panjang tali terpanjang = U5 = ar4 = 160
banyak bagian tali = n = 5
Ini berarti panjang tali semula adalah jumlah panjang kelima bagian tali (S5).
Mula-mula tentukan nilai r dengan mengganti a = 10, n = 5 dan U5 = 160 ke rumus Un.

Selanjutnya tentukan panjang panjang tali semula (S5) yaitu
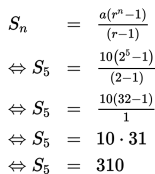
Jadi, panjang tali semula adalah 310 cm.
soal no 9
soal no 9
Sebuah bola dijatuhkan dari ketinggian 4 meter. Kemudian bola tersebut
memantul kembali setinggi 3 meter dan seterusnya. Setiap kali menyentuh
lantai, bola tersebut akan memantul setinggi 34 kali ketinggian sebelumnya. Tentukan panjang lintasan yang terbentuk sampai bola menyentuh lantai untuk yang ke-3 kalinya.
Penyelesaian:
Perhatikan ilustrasi berikut.

Berdasarkan ilustrasi, tampak bahwa ketika bola dijatuhkan dan menyentuh
lantai untuk yang ke 3 kali sesungguhnya bola tersebut mengalami 3 kali gerakan turun (panah merah) dan 2 kali gerakan naik (panah biru).
• Barisan yang terbentuk saat bola turun (ditunjukkan oleh panah warna merah) adalah 4,(34 ) 4, (34)2 (4),... = 4, 3, 94 , ....
Barisan ini adalah barisan geometri turun dengan a = 4 dan r =34
Oleh karena terdapat 3 kali gerakan turun (n = 3), maka panjang lintasan yang terbentuk saat bola turun (S3) adalah
Oleh karena terdapat 3 kali gerakan turun (n = 3), maka panjang lintasan yang terbentuk saat bola turun (S3) adalah
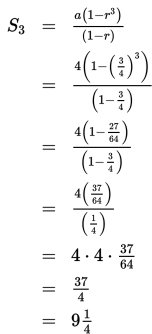
- Barisan yang terbentuk saat bola naik (ditunjukkan oleh panah warna biru) adalah (
34 ) 4 ,(34)2 (4), ... = 3,94 , ....
Barisan ini adalah barisan geometri turun dengan a = 3 dan r =
Oleh karena terdapat 2 kali gerakan naik (n = 2), maka panjang lintasan yang terbentuk saat bola naik (S2) adalah

Jadi, panjang lintasan yang terbentuk sampai bola menyentuh lantai untuk yang ke 3 kalinya adalah 14, 5 meter.
Latihan
- Tentukan suku ke 10 dari barisan 1/8, 1/4, 1/2, ….
- Sebuah amoeba dapat membelah diri menjadi 2 setiap 6 menit. Pertanyaannya, berapakah jumlah amoeba setelah satu jam jika pada awalnya terdapat 2 amoeba?
- Tentukan tiga suku pertama pada barisan-barisan berikut ini, jika suku umum ke-n di rumuskan sebagai berikut: a. Un = 4n+1 b. Un = 2n2 – 1 c. Un = 1 – 2n
- Tentukan rumus umum ke – n dari barisan-barisan berikut ini: a. 2, 4, 8, 16, 32, …
- Diketahui barisan geometri, U2=14 dan U4=56, tentukan a dan rasionya?
b. 4, 6, 8, 10, …
Langganan:
Komentar (Atom)






















