BARISAN DAN DERET GEOMETRI

BARISAN GEOMETRI

Barisan geometri merupakan barisan yang suku-sukunya diperoleh dengan mengalikan satu bilangan tetap ke suku sebelumnya. Bilangan tetap itu sering disebut sebagai pembanding atau rasio yang dilambangkan dengan r.

Barisan U1 , U2 , U3 , U4 , ….. , Un disebut sebagai barisan geometri jika memenuhiRasio

Contoh barisan geometri :
7, 21, 63, 189, ....
3, 6, 12 , 24, 48 ,. . . .

Rumus Suku ke-n

Jika suku pertama ( U1 ) dari suatu barisan geometri disimbolkan dengan a , maka rumus suku ke-n barisan geometri dapat ditentukan sebagai berikut:

Dari pernyataan diatas, dapat ditarik kesimpulan bahwa rumus suku ke-n dari suatu barisan geometri adalah

Dimana r adalah rasio atau pembanding yang dapat dicari dengan cara berikut:

Contoh Soal :

1. Tentukan suku ke tujuh dari barisan geometri 3, 6, 12, .....!


2. Tentukan Rumus Suku ke-n dari barisan 48 , 24 , 12 , ……!


3. Dari barisan geometri diketahui bahwa U3 = 4 dan U9 = 256, maka tentukan U12!


4. Tiga buah bilangan membentuk barisan geometri. Jumlah ketiga bilangan tersebut sama dengan 35, sedangkan hasil kali ketiga bilangan itu sama dengan 1.000. Maka tentukan barisan geometri tersebut!

Jawab :

1. Dari Barisan 3, 6, 12, ... didapat a = 3 dan r = 6/3 = 2 sehingga,

Un = a.r^n-1
U7 = 3.2
U7 = 3.2⁶
U7 = 3.64
U7 = 192

1. Dari barisan 48, 24, 12, .... didapat a = 48 dan r = 24/48 = 1/2 sehingga,

Un = a.r^n-1
Un = 48.(1/2)^n-1
Un = 48.(1/2)^n-1
Un = 48.(2^-1)^1-n
Un = 3.16.(2)^1-n
U7 = 3.2⁴(2)^1-n
U7 = 3.2^5-n


2. Pertama, kita jabarkan terlebih dahulu U3 dan U9 kemudian kita cari nilai rasionya
   
   U3 = 4 → a.r² = 4
   U9 = 256 → a.r⁸ = 256

Kemudian substitusikan untuk mencari U1 atau a!

→ a.r² = 4
→ a.2² = 4
→ a = 1
Next, cari nilai U12 dengan menggunakan rumus umum barisan geometri!
U₁₂ = a.r^n-1
U12 = 1.2¹¹
U12 = 1.2048
U12 = 2048

3. jawaban soal no 4

DERET GEOMETRI

Jumlah dari n suku pertama suatu barisan geometri disebut sebagai deret geometri. Jika suku ke-n dari barisan geometri dirumuskan: a_n = a₁r^{n – 1}, maka deret geometri dapat dituliskan sebagai,

Jika kita mengalikan deret tersebut dengan –r kemudian menjumlahkannya dengan deret aslinya, kita mendapatkan

Sehingga kita memperoleh Sn – rSn = a1 – a1rn. Dengan menyelesaikan persamaan tersebut untuk Sn, kita mendapatkan

Rumus suku ke n



Contoh Soal:

1. Tentukan jumlah 10 suku pertama dari deret 32 + 16 + 8 + ….!
2. Tentukan nilai n yang memenuhi2 + 2² + 2³ + ….. + 2ⁿ = 510!

Jawab:

1. Dari deret 32 + 16 + 8 + .... didapat a = 32 dan r = 1/2, sehingga

2. Dari deret 2 + 2² + 2³ + ….. + 2ⁿ = 510 didapat a = 2 dan r = 2, sehingga

Soal No. 3
Diberikan sebuah deret geometri sebagai berikut.
3 + 6 + 12 + ....
Tentukan suku ke-5 dari deret tersebut!
Pembahasan
Rumus suku ke-n deret geometri
U_n = ar^{n −1}

dimana
a = suku pertama
r = rasio

Dari soal
a = 3
r = ⁶/₃ = 2

sehingga
U_n = arⁿ⁻¹
U₅ = 3 (2)^{5 −1} = 3 (2)⁴ = 3(16) = 48

Soal No. 4
Diketahui suku pertama suatu deret geometri adalah 4 dengan suku ke-5 adalah 324. Tentukan rasio dari deret tersebut!

Pembahasan
Data dari soal di atas
U₅ = 324
a = 4

Dari U_n = ar^{n −1}

Dengan demikian rasionya adalah 3 atau − 3

Soal No. 5
Deret geometri 12 + 6 + 3 + ....
Tentukan U₃ + U₅

Pembahasan
U₃ = 3
a = 12
r = ⁶/₁₂ = ¹/₂

Un = ar^{n −1}
U₅ = 12(1/2)^{5 −1} = 12(1/2)⁴ = 12(1/16) = 12/16 = 3/4

Sehingga
U₃ + U₅ = 3 + ³/₄ = 3 ³/₄

Soal No. 6
Diberikan sebuah deret geometri sebagai berikut.
3 + 6 + 12 + ....
Tentukan jumlah 7 suku pertama dari deret tersebut!

Pembahasan
Data:
a = 3
r = ⁶/₃ = 2
S₇ =....

Rumus mencari jumlah n suku pertama deret geometri untuk rasio lebih besar dari satu r > 1


Sehingga:










Soal No. 7
Diberikan sebuah deret geometri sebagai berikut.
24 + 12 + 6 +...
Tentukan jumlah 7 suku pertama dari deret tersebut!

Pembahasan
Data:
a = 24
r = ¹²/₂₄ = ¹/₂
S₇ =....

Rumus mencari jumlah n suku pertama deret geometri untuk rasio lebih kecil dari satu r < 1

 Sehingga:


 


















soal no 8

Seutas tali dibagi menjadi 5 bagian yang panjangnya membentuk barisan geometri.
Jika tali yang paling pendek adalah 10 cm dan tali yang paling panjang adalah 160 cm, tentukan panjang tali semula.

Penyelesaian:

Diketahui potongan-potongan tali membentuk barisan geometri, dengan:
panjang tali terpendek = U1 = a = 10
panjang tali terpanjang = U5 = ar4 = 160
banyak bagian tali = n = 5

Ini berarti panjang tali semula adalah jumlah panjang kelima bagian tali (S5).

Mula-mula tentukan nilai r dengan mengganti a = 10, n = 5 dan U5 = 160 ke rumus Un.

Selanjutnya tentukan panjang panjang tali semula (S5) yaitu

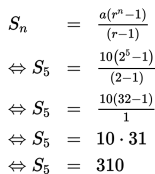
Jadi, panjang tali semula adalah 310 cm.

soal no 9

Sebuah bola dijatuhkan dari ketinggian 4 meter. Kemudian bola tersebut memantul kembali setinggi 3 meter dan seterusnya. Setiap kali menyentuh lantai, bola tersebut akan memantul setinggi 34$\frac{3}{4}$ kali ketinggian sebelumnya. Tentukan panjang lintasan yang terbentuk sampai bola menyentuh lantai untuk yang ke-3 kalinya.

Penyelesaian:

Perhatikan ilustrasi berikut.

Berdasarkan ilustrasi, tampak bahwa ketika bola dijatuhkan dan menyentuh lantai untuk yang ke 3 kali sesungguhnya bola tersebut mengalami 3 kali gerakan turun (panah merah) dan 2 kali gerakan naik (panah biru).

• Barisan yang terbentuk saat bola turun (ditunjukkan oleh panah warna merah) adalah 4,(34$\frac{3}{4}$) 4, (34)2$(\frac{3}{4}{)}^2$ (4),... = 4, 3, 94$\frac{9}{4}$, ....

Barisan ini adalah barisan geometri turun dengan a = 4 dan r =34$\frac{3}{4}$
Oleh karena terdapat 3 kali gerakan turun (n = 3), maka panjang lintasan yang terbentuk saat bola turun (S3) adalah

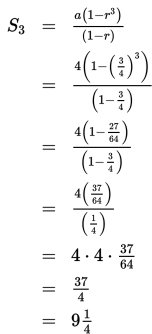
• Barisan yang terbentuk saat bola naik (ditunjukkan oleh panah warna biru) adalah (34$\frac{3}{4}$) 4 , (34)2$(\frac{3}{4}{)}^2$ (4), ... = 3, 94$\frac{9}{4}$, .... 

Barisan ini adalah barisan geometri turun dengan a = 3 dan r =34$\frac{3}{4}$

Oleh karena terdapat 2 kali gerakan naik (n = 2), maka panjang lintasan yang terbentuk saat bola naik (S2) adalah

Jadi, panjang lintasan yang terbentuk sampai bola menyentuh lantai untuk yang ke 3 kalinya adalah 14, 5 meter.

Latihan

1. Tentukan suku ke 10 dari barisan 1/8, 1/4, 1/2, ….


2. Sebuah amoeba dapat membelah diri menjadi 2 setiap 6 menit. Pertanyaannya, berapakah jumlah amoeba setelah satu jam jika pada awalnya terdapat 2 amoeba?


3. Tentukan tiga suku pertama pada barisan-barisan berikut ini, jika suku umum ke-n di rumuskan sebagai berikut: a. Un = 4n+1 b. Un = 2n2 – 1 c. Un = 1 – 2n


4. Tentukan rumus umum ke – n dari barisan-barisan berikut ini:
a. 2, 4, 8, 16, 32, …
b. 4, 6, 8, 10, …

5. Diketahui barisan geometri, U2=14 dan U4=56, tentukan a dan rasionya?